DARwIn-OP Education
TP1 SII PTSI 1 CI7
Document professeur
Centre d'intrt N¡ 7 :
Proposer un modle gomtrique et cinmatique des
mouvements entre solides indformables dÕun systme

Constitution de lÕlot
¤ Un robot DarwIn-OP instrument en tat de fonctionnement ;
¤ Un ordinateur de pilotage et dÕacquisition associ au robot DarwIn-OP ;
¤ Plusieurs postes de travail constitus chacun dÕun ordinateur
communicant avec lÕordinateur de pilotage.
Vous trouverez dans ce document Professeur :
¤ La fiche tudiant ;
¤ Le droulement des activits ;
¤ La fiche de formalisation ;
¤ Le dossier rponses ;
¤ La rponse technique ;
¤ La fiche dÕauto-valuation.
FICHE
ETUDIANT
1. La problmatique pose l'quipe
Fournir lÕanalyste
programmeur du bureau dÕtudes (dveloppeur de logiciels) les outils
(rsultats) ncessaires la comprhension et la commande dÕun membre du
robot DARwIn-OP, via les servomoteurs, afin dÕeffectuer la tche demande selon
un point de vue gomtrique.
Pour obtenir ces rsultats il
faut franchir plusieurs tapes. Dans ce TP1 CI7 ne seront abords que trois
tapes sur les quatre ncessaires pour rpondre compltement la
problmatique. La rponse technique sera donc partielle. Le TP2 CI7 concerne la
quatrime tape.
2. La description des activits pendant la
sance
En prsence du robot DARwIn-OP
associ un ordinateur connect Internet et implant au sein d'un lot.
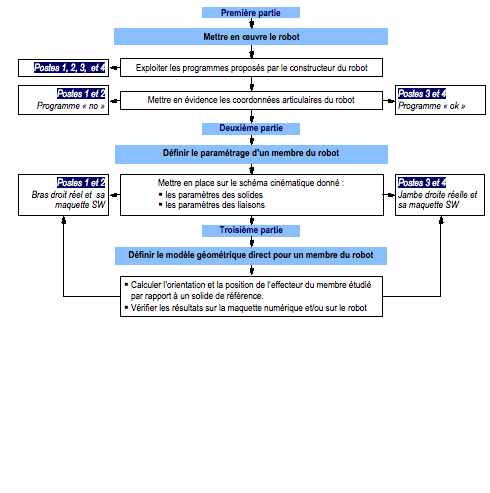
LÕquipe travaillant sur l'lot doit :
L'quipe travaillant sur l'lot doit rendre :
Un document
technique (rponse technique) dfinissant le schma paramtr et les rsultats
exprimant le modle gomtrique direct dÕun membre du robot ncessaire au
bureau dÕtudes.
Chaque tudiant doit rdiger :
Une fiche de
formalisation des connaissances qui dtaille la dmarche suivre pour obtenir
le modle gomtrique direct du membre considr et une fiche
d'auto-valuation.
3. Les prrequis
¤
Schmatisation dÕune liaison pivot normalise et repre associ.
¤ Paramtrage dÕun systme mcanique
dans le but dÕlaborer un modle gomtrique (ou cinmatique).
-
Paramtrage des solides
A chaque solide du mcanisme considr est associ
un repre. Dans ce repre la position des centres de liaison est dfinie par
les paramtres gomtriques constants.
-
Paramtrage des liaisons
A chaque liaison est associ autant de paramtres
gomtriques variables que la liaison comporte de degrs de libert.
Au solide Si+1 est associ le repre ![]() et au solide Si le repre
et au solide Si le repre![]() . LÕassociation privilgie les axes de la liaison ainsi pour
une liaison pivot entre les deux solides Si+1 et Si,
lÕaxe de la liaison, sont associs les vecteurs unitaires
. LÕassociation privilgie les axes de la liaison ainsi pour
une liaison pivot entre les deux solides Si+1 et Si,
lÕaxe de la liaison, sont associs les vecteurs unitaires![]() .
.
Dans le plan la base Bi+1 associe
au solide Si+1 se dduit de la base Bi associe au solide
Si par une rotation
![]() autour de lÕaxe
autour de lÕaxe![]() avec
avec ![]()
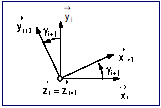
LÕangle ![]() est nomm coordonne articulaire de la liaison
entre les solides Si+1 et Si.
est nomm coordonne articulaire de la liaison
entre les solides Si+1 et Si.
Le
choix des origines des repres dpend du type de liaison considr. Pour une
liaison pivot les origines des repres associs aux solides sont choisies
confondues et places sur lÕaxe de la liaison.
Remarque :
Afin dÕviter les erreurs de calcul lÕangle dÕorientation dÕune base par rapport
une autre doit tre dessin aigu et positif.
La
matrice de changement de base qui exprime les coordonnes de la base Bi+1
dans la base Bi sÕcrit :
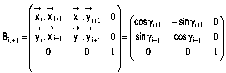
Il peut tre utile dÕcrire le changement de base
sous la forme
La lecture en ligne donne les composantes dans la
base Bi des vecteurs de la base Bi+1.
La lecture en colonne donne les composantes dans la
base Bi+1 des vecteurs de la base Bi.
De
mme si dans le plan un vecteur ![]() est repr par
est repr par ![]() alors
alors
La lecture en ligne donne les composantes dans la
base Bi de ![]() dans la base Bi+1.
dans la base Bi+1.
La lecture en colonne donne les composantes dans la
base Bi+1 de ![]() dans la base Bi.
dans la base Bi.
¤
Relation de Chasles sur les angles dans le plan
Dans le plan, pour tous vecteurs non nuls ![]() ,
,![]() et
et![]() on a la relation suivante (dite de Chasles) sur les angles
on a la relation suivante (dite de Chasles) sur les angles
![]()
¤
Relation de Chasles sur les positions dans le cas gnral
Pour trouver la position du point ![]() appartenant au
solide
appartenant au
solide ![]() par rapport au repre
par rapport au repre ![]() li au solide
li au solide ![]() on dfini le vecteur position
on dfini le vecteur position ![]() en
appliquant la relation de Chasles
en
appliquant la relation de Chasles
![]()

Les coordonnes
cartsiennes de ![]() dans le repre
dans le repre ![]() sont
sont ![]() telles que
telles que ![]() .
.
¤ Classe dÕquivalence
Une classe dÕquivalence est un ensemble de pices
qui nÕont aucun mouvement relatif entre elles pour la phase de fonctionnement
considre. DÕaucuns utilisent la locution "groupe cinmatiquement li"
pour dfinir un ensemble de pices lies par encastrement. Il est
alors possible dÕen donner une reprsentation indiffrencie sur un schma
cinmatique ou un graphe des liaisons.
4. Les savoir-faire dvelopps
¤
Associer un repre un
solide ;
¤
Identifier les degrs de libert dÕun
solide en mouvement par rapport un repre ;
¤
Raliser le paramtrage dÕun
mcanisme simple ;
¤
Prendre en compte les restrictions
de mouvement pour simplifier les modles ;
¤
Ecrire le vecteur position dÕun
point dÕun solide dans le systme de coordonnes cartsiennes.
5. Les connaissances
Proposer un modle
¤ Modles
de solide
Modle de solide indformable ;
¤ Modlisation
gomtrique et cinmatique des mouvements entre solides indformables
Dplacement des points dÕun solide : repre
li un solide, paramtres gomtriques linaires et angulaires dfinissant la
position d'un solide par rapport un autre, dplacements d'un solide.
6. Avant de commencer
L'quipe doit vrifier que les ressources ncessaires la
ralisation des activits pratiques sont prsentes au sein de lÕlot [1].
¬ Le robot DARwIn-OP
fonctionnel associ lÕordinateur de pilotage et connect au rseau avec son
support.
¬ Plusieurs postes de
travail constitus chacun d'un ordinateur communicant avec l'ordinateur de
pilotage et d'acquisition.
Ressources
logicielles et numriques :
¬ Modle 3D sous le format
SolidWorks du robot complet, ainsi que de chaque membre spar.
L'ensemble des ressources est disponible ? Oui / Non
Si oui,
alors passer l'tape suivante.
Si non,
faite appel votre professeur pour que les ressources ncessaires soient
misent votre disposition avant de passer l'tape suivante.
DEROULEMENT
DES ACTIVITES
Problme pos
l'quipe
Un robot humanode doit pouvoir se mouvoir dans un espace humain, avec
des dplacements et des gestes particuliers qui correspondent aux diffrentes tches
quÕil aura accomplir.
Le robot DARwIn-OP tant destin au service la personne, il doit par
exemple tre capable de porter un verre plein sans le renverser, tout en
montant un escalierÉ Comment
commander ce type de robot pour quÕil excute les mouvements voulus ?
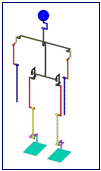 Tout robot humanode est constitu dÕun
assemblage de segments relis par des articulations, gnralement motorises.
Tout robot humanode est constitu dÕun
assemblage de segments relis par des articulations, gnralement motorises.
Les liaisons sont ici des articulations rotodes (liaisons pivot) fig. 1.
Les Ç muscles È du robot, ses
actionneurs, utilisent une nergie lectrique et les actions mcaniques et
mouvements produits par les moteurs sont transmis aux articulations par un
rducteur engrenages.
Avant mme de vouloir faire bouger ce robot, il importe de savoir comment
le reprer, cÕest--dire caractriser gomtriquement ses positions et sa
relation la tche accomplir.
On doit donc dans un premier temps dfinir Ç directement È la
position et lÕorientation exacte que doit avoir un membre dans lÕespace
oprationnel, pour excuter la tche. Or, ce sont des moteurs qui mettent en
mouvements les articulations du robot. On a donc besoin de dfinir galement
les coordonnes dites Ç articulaires È du robot afin de pouvoir le
commander.
Nous allons chercher fournir au bureau dÕtude les lments ncessaires
lÕtude de la gomtrie dÕun membre du robot selon une dmarche de
lÕingnieur (fig. 2).
![]()
![]()
![]()
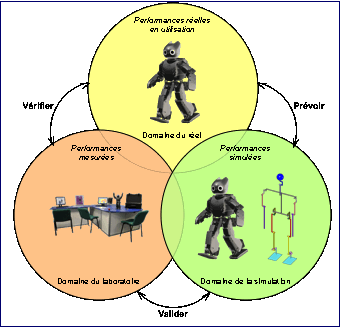
fig. 1 : Schma 3D du robot
DarwIn-OP
fig. 2 : La dmarche de
l'ingnieur
1re Partie
Postes 1, 2, 3 et 4
Objectif
Manipuler et mettre en vidence les coordonnes articulaires des membres
du robot.
Le robot DARwIn doit tre aliment et reli
lÕordinateur afin que vous puissiez communiquer avec lui.
Le
cblage et la commande du robot sont dtaills dans le dossier ressources
techniques.
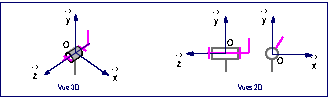
La fig. 3 donne un servomoteur en vue de
face. La base ![]() est associe au
carter c du servomoteur. La base
est associe au
carter c du servomoteur. La base ![]() est associe
lÕarbre de sortie s du servomoteur. Le vecteur unitaire
est associe
lÕarbre de sortie s du servomoteur. Le vecteur unitaire ![]() fixe le
Ç 0 È du servomoteur ainsi les sens + et – de lÕangle de
rotation de lÕarbre de sortie par rapport au carter sont parfaitement dfinis.
fixe le
Ç 0 È du servomoteur ainsi les sens + et – de lÕangle de
rotation de lÕarbre de sortie par rapport au carter sont parfaitement dfinis.
Le capteur de position
intgr au servomoteur est un codeur absolu dont la rsolution est de 4096 points
par tour. La valeur indique pour la position de chaque servomoteur dans le
logiciel est en point, avec une valeur mdiane de 2048.
Si p correspond
lÕangle de rotation de lÕarbre de sortie s par rapport au carter c en point
et ![]() la valeur en ¡ alors :
la valeur en ¡ alors :
![]()
et
![]()
Toute modification dÕun point positif, fera tourner
lÕarbre de sortie du servomoteur dÕun pas dÕenviron 0,0879¡.
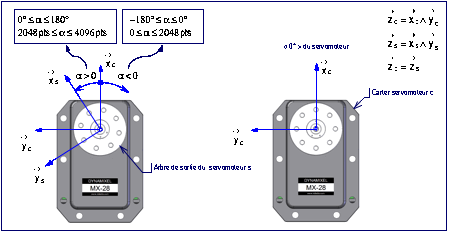
fig. 3 : Repres associs au servomoteur
Le robot est
pralablement plac sur son support (fig. 4).

fig. 4 : Robot
sur son support
Les rponses sont
fournir dans le dossier rponses.
Postes 1 et 2
Lancer le programme Ç no È
et observer les modifications des valeurs de position des servomoteurs.
Q 1 : Quel numro de servomoteur permet
dÕobtenir le mouvement du cou ?
Le bras droit fig. 5 est actionn
par les trois servomoteurs numrots 1, 3 et 5.
¤
Slectionner le servomoteur 1 ;
¤
Modifier la valeur de sa position grce au potentiomtre
(augmenter de 200 points par exemple), et appliquer cette valeur.
Q
2 : En observant le mouvement rsultant, identifier lÕaxe
correspondant.
Q 3 : Faire de mme pour les autres
servomoteurs.
Modifier nouveau les valeurs
pour retrouver la configuration initiale (diminuer de 200 points par exemple)
Q 4 : Quelle
valeur faut-il proposer pour que le servomoteur 1 tourne dÕenviron +90¡
partir de la position impose par le programme de mise en position initiale.
Tester votre rsultat avec le
logiciel de commande.
Replacer lÕpaule du robot dans sa
position initiale en imposant nouveau la valeur initiale.
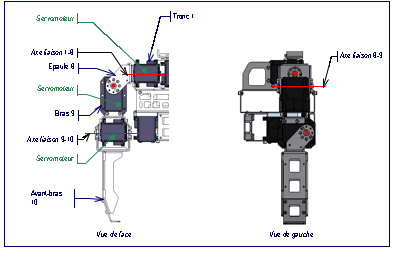
fig. 5 :
Elments du bras droit
Postes 3 et 4
Lancer le programme Ç ok È et observer les
modifications des valeurs de position des servomoteurs.
Q
1 : Quel numro de servomoteur
permet dÕobtenir ce mouvement de la tte ?
La jambe droite fig. 6 est
actionne par les six servomoteurs numrots 7, 9, 11, 13, 15 et 17 .
¤
slectionner le servomoteur 11 ;
¤
modifier la valeur de sa position grce au potentiomtre
(augmenter de 200 points par exemple), et appliquer cette valeur.
Q 2 : En observant
le mouvement rsultant, identifier quel est lÕaxe correspondant.
Q 3 : Faire de
mme pour les servomoteurs 13 et 15.
Modifier nouveau les valeurs
pour retrouver la configuration initiale (diminuer de 200 points par exemple).
Q 4 : Quelle
valeur faut-il proposer pour que le servomoteur 17 correspondant la rotation du pied droit de lÕextrieur vers
lÕintrieur de la jambe lorsquÕon augmente le pas, tourne dÕenviron de +45¡ ?
Tester votre rsultat avec le
logiciel de commande.
Replacer le robot dans sa position
initiale en imposant nouveau la valeur initiale.
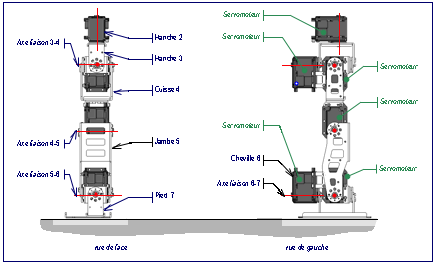
fig. 6 : Elments de la jambe
droite
2me Partie
Objectif :
Mettre en
place le paramtrage gomtrique dÕun membre du robot.
Remarque :
La faon de paramtrer un systme mcanique nÕest pas unique. Le paramtrage
qui est propos par la suite est celui dit de Denavit-Hartenberg utilis
gnralement par les roboticiens.
Le mouvement relatif
la marche humaine met en jeu divers dplacements, qui se droulent dans
diffrents plans illustrs dans la fig. 7. Ces dplacements constituent des
facteurs biomcaniques intervenant principalement dans le plan sagittal et dans
le plan frontal (ou coronal). Ils garantissent la stabilit de l'unit
locomotrice et lui permettent le synchronisme mobilit/stabilit. Nous
utiliserons le vocabulaire de ces plans dans ce TP.
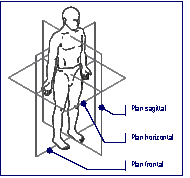
fig. 7 : Plans caractristiques de
la biomcanique
Les rponses de cette
partie sont fournir dans le document de la rponse technique.
Le trac du schma du
membre considr dans un plan parallle au plan sagittal suppose une hypothse
relative lÕune des coordonnes articulaires ou revient considrer que deux
solides sont en liaison encastrement dans une position particulire (classe
dÕquivalence). Cette hypothse est
retenue pour tout le TP.
Q 5 :
Citer la classe dÕquivalence concerne et ses caractristiques gomtriques.
Q 6 : Pour le membre
concern mettre en place sur le document rponse technique :
¤
les repres associs aux diffrents solides ;
¤
les coordonnes articulaires sachant que ![]() dsigne la
coordonne articulaire du solide i par rapport au solide i-1 ;
dsigne la
coordonne articulaire du solide i par rapport au solide i-1 ;
¤
les coordonnes constantes lis aux solides.
Q 7 : Mesurer sur le robot ou/et
sur la maquette numrique du membre concern les paramtres gomtriques
constants
Postes 1 et 2
Paramtrage du bras
droit
La fig. 8 donne le schma cinmatique plan et la fig. 9 prcise les repres associs aux
solides du bras droit.
On note les distances
![]() ;
;
![]()
![]()
![]()
et
![]()
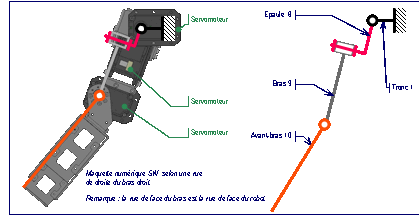
fig. 8 : Schma
cinmatique plan du bras droit
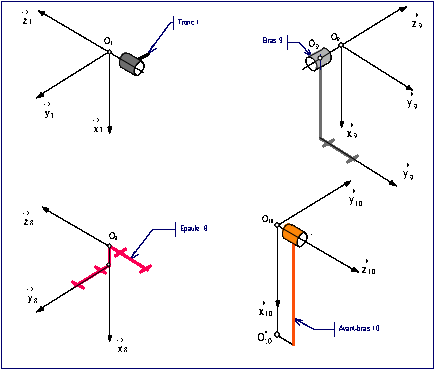
fig. 9 :
Modlisation des solides du bras droit
Postes 3 et 4
Paramtrage de la jambe
droite
La fig. 10 donne le schma cinmatique plan et
la fig. 11 prcise les repres associs aux
solides de la jambe droite.
On note les distances :
![]()
![]()
![]()
![]()
et
![]()
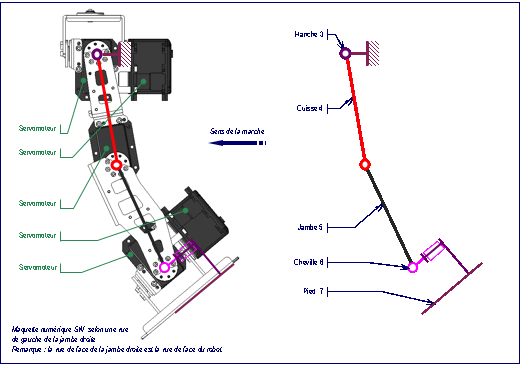
fig. 10 : Schma cinmatique plan
de la jambe droite
fig. 11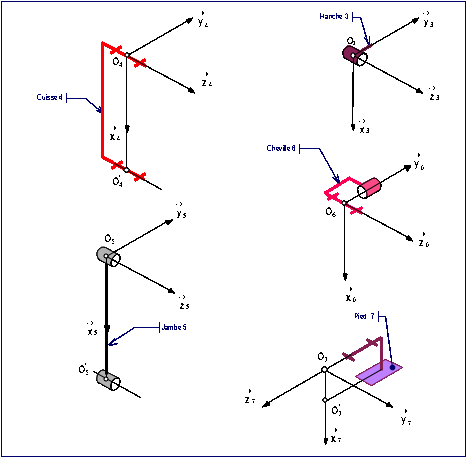
: Modlisation des solides des solides de la jambe droite
3me Partie
Objectif :
Dfinir le
modle gomtrique direct du membre considr
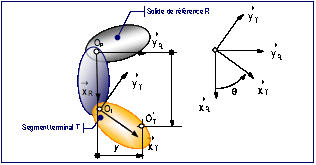
Pour
une structure plane en chane ouverte de
solides (fig. 12) lÕorientation de lÕeffecteur T par
rapport a un solide de rfrence R se rduit un angle que lÕon notera ![]() tel que
tel que
![]()
et
les coordonnes cartsiennes du point ![]() li au segment
terminal T dans le repre R se rduisent aux coordonnes que lÕon notera x
et y telles que
li au segment
terminal T dans le repre R se rduisent aux coordonnes que lÕon notera x
et y telles que
![]()
![]()
fig. 12 : Exemple de paramtrage
Dans le plan les coordonnes cartsiennes x,
y et lÕangle ![]() donnent respectivement la position et lÕorientation du
segment terminal par rapport au solide de rfrence.
donnent respectivement la position et lÕorientation du
segment terminal par rapport au solide de rfrence.
Les rponses aux questions de cette partie sont
rdiger sur feuille de copie. Les rsultats littraux seront nots dans la
rponse technique.
Q 8 : Dterminer pour le membre considr le modle
gomtrique direct.
Postes 1 et 2
On considre le bras droit.
Le solide de rfrence est le tronc 1 et le segment
terminal est lÕavant-bras 10.
Il sÕagit donc de trouver lÕorientation de la base
associe lÕavant-bras 10 et les coordonnes cartsiennes du point ![]() par rapport au
repre li au tronc 1, c'est--dire
par rapport au
repre li au tronc 1, c'est--dire![]() , x et y en fonction des coordonnes
articulaires et des paramtres lis aux pices.
, x et y en fonction des coordonnes
articulaires et des paramtres lis aux pices.
Q 9 : Application numrique
On donne :
![]()
![]()
Modle gomtrique direct (MGD)
Le
bras 9 li compltement lÕpaule 8 tel que ![]()
La position du point ![]() dans le repre li au tronc 1 sÕexprime partir de la
relation de Chasles
dans le repre li au tronc 1 sÕexprime partir de la
relation de Chasles
![]()
avec
![]()
![]()
![]()
![]()
alors
![]()
Le point atteindre est tel que
![]()
alors
![]()
![]()
soit
![]() (1)
(1)
![]() (2)
(2)
Les relations (1) et (2) fournissent les
coordonnes cartsiennes du point ![]() dans le repre
dans le repre ![]()
LÕavant-bras 10 par rapport au torse 1
est globalement orient par
![]() (relation de
Chasles sur les angles)
(relation de
Chasles sur les angles)
Application numrique :
Avec les valeurs trouves en 1re
partie :![]() ,
,![]() ,
, ![]() ,
, ![]() et les coordonnes articulaires imposes
et les coordonnes articulaires imposes ![]() et
et ![]()
alors (1) et (2) donnent :
![]()
![]()
![]()
![]()
et ![]()
![]()
![]()
Postes 3 et 4
On considre la jambe droite.
Le solide de rfrence est la hanche 3 et le
segment terminal est le pied 7.
Il sÕagit donc de trouver lÕorientation de la base
associe au pied 7 et les coordonnes cartsiennes du point ![]() par rapport au
repre li la hanche 3 :
par rapport au
repre li la hanche 3 : ![]() , c'est--dire
, c'est--dire![]() , x et y en fonction des coordonnes
articulaires et des paramtres lis aux pices.
, x et y en fonction des coordonnes
articulaires et des paramtres lis aux pices.
Q 9 : Application numrique
On donne :
![]()
![]()
![]()
Modle
gomtrique direct (MGD)
La
cheville 6 et le pied 7 sont lis compltement tel que ![]()
La position du point ![]() dans le repre li la hanche 3 sÕexprime partir de la
relation de Chasles
dans le repre li la hanche 3 sÕexprime partir de la
relation de Chasles
![]()
avec ![]()
![]()
![]()
![]()
![]()
soit ![]()
Le point atteindre est tel que
![]()
alors ![]()
![]()
soit ![]() (1)
(1)
![]() (2)
(2)
et lÕorientation du pied 7 est fixe par
![]()
donc en appliquant la relation de Chasles
sur les angles
![]() (3)
(3)
Les relations (1) et (2) fournissent les
coordonnes cartsiennes du point ![]() dans le repre
dans le repre ![]()
La relation (3) donne lÕorientation du
pied 7 par rapport la hanche 3.
Application numrique :
Avec les valeurs
trouves en 1re partie : ![]() et
et ![]() et les coordonnes articulaires donnes
et les coordonnes articulaires donnes ![]() ,
, ![]() ,
, ![]() , alors
, alors
![]()
![]()
![]()
![]()
![]()
![]()
![]() (
(![]() )
)
Lancer le programme
Ç Walkready È afin de placer le robot dans la configuration initiale souhaite, sÕil
nÕy est pas dj.
Dans cette configuration
le robot est debout, dans une position Ç initiale È, bras plis, et
prt marcher. Les valeurs du constructeur pour les positions de chaque
servomoteur sont donnes fig. 13.
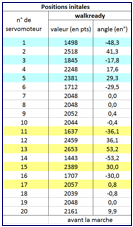
fig. 13 : Valeurs initiales des
servomoteurs avant la marche (Ç walkready È)
Le robot repose sur un
sol plan suppos horizontal auquel est associ un repre de base![]() . Le vecteur unitaire
. Le vecteur unitaire![]() est celui de la
verticale descendante, le vecteur unitaire
est celui de la
verticale descendante, le vecteur unitaire![]() est orient dans le sens de la marche.
est orient dans le sens de la marche.
Les membres tudis du robot doivent respecter
lÕhypothse formule en dbut de TP c'est--dire quÕils doivent tre dans un
plan parallle au plan sagittal.
Les axes associs aux servomoteurs concerns sont
ceux de la fig. 3. Sur les figures suivantes ils sont
reprsents en bleu.
Postes 1 et 2
La fig. 14 reprsente le modle sous Solidworks
du bras droit selon une vue de gauche dans la position initiale et le schma
associ avec les deux servomoteurs concerns. Les servomoteurs 1 et 5 sont
rgls approximativement sur les valeurs donnes par le constructeur,
respectivement ![]() et
et![]() .
.
Rgler le servomoteur 3 dans la position 1536
points afin dÕobtenir lÕensemble du bras dans un plan parallle au plan
sagittal.
La position du point ![]() en position
initiale est dfinie par le vecteur position
en position
initiale est dfinie par le vecteur position
![]() dans le repre
dans le repre ![]()
Par rapport la base associe au sol le tronc 1
est inclin dÕun angle ![]() (fig. 14) tel que
(fig. 14) tel que ![]() .
.
Q
10 :
Comparer les rsultats trouvs et
les coordonnes articulaires donnes la question Q 9 et les rsultats donns par une
simulation du robot. Pour cela :
¤ identifier et conclure quant aux
coordonnes articulaires ;
¤ retrouver les coordonnes![]() et
et![]() donnes sur la fig. 14 ;
donnes sur la fig. 14 ;
¤ vrifier approximativement la position
du point ![]() sur le robot ;
sur le robot ;
¤ conclure propos des valeurs simules, mesures et calcules.
![]()
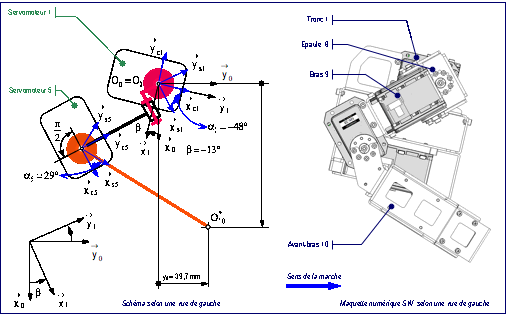
fig. 14 : Position du bras droit
avant la marche (Ç walkready È)
LÕexamen des donnes de lÕapplication
numrique de la question Q 9
et
des fig. 13 et fig. 14 permet de conclure que :
![]()
mais que ![]() et
et ![]() , car par construction
, car par construction ![]() est
perpendiculaire
est
perpendiculaire ![]() dÕo
dÕo ![]()
Ces valeurs correspondent
approximativement celles donnes par la fig. 13.
Les coordonnes ![]() et
et ![]() donnes
dans le repre
donnes
dans le repre ![]() sur la fig.
14 diffrent des
valeurs de x et y exprimes dans le repre
sur la fig.
14 diffrent des
valeurs de x et y exprimes dans le repre ![]() car globalement lÕensemble du bras a tourn de lÕangle
car globalement lÕensemble du bras a tourn de lÕangle![]() .
.
Pour retrouver les coordonnes du point![]() dans le repre li au
sol posons
dans le repre li au
sol posons
![]()
et ![]()
avec
alors ![]()
soit avec les valeurs donnes et celles
trouves prcdemment, on obtient
![]()
![]()
![]()
LÕorientation de lÕavant-bras par rapport
au tronc tait ![]() alors compte tenu
de lÕorientation du tronc elle devient
alors compte tenu
de lÕorientation du tronc elle devient ![]()
Les valeurs calcules ci-dessus sont
approximativement celles du modle solidworks et celles mesures sur le robot.
La mesure sur le robot est peu prcise
(dpend en tout cas des moyens de mesure)
Les
positionnements angulaires des servomoteurs choisis pour les calculs et la
simulation sous Solidworks ne sont nÕest pas exactement ceux fournis par le
constructeur et les coordonnes articulaires donnes par le robot varient au
cours du temps.
Postes 3 et 4
La fig. 15 reprsente le modle sous Solidworks de
la jambe droite et le schma avec les servomoteurs, selon une vue de droite
dans la position initiale. On considre que les servomoteurs 7, 9 et 17 sont
rgls sur la valeur 0¡ approximative c'est--dire que la jambe est suppose
tre dans un plan parallle au plan sagittal.
Les
servomoteurs 11, 13 et 15 sont rgls sur les valeurs approximatives, respectivement![]() ,
, ![]() et
et![]() .
.
La position du point ![]() est dfinie par
le vecteur position dans le repre
est dfinie par
le vecteur position dans le repre ![]()
![]()
Par rapport la base associe au sol le tronc 1
est inclin dÕun angle ![]() qui fait intervenir une base auxiliaire
qui fait intervenir une base auxiliaire ![]() telle que
telle que ![]() et
et ![]() .
.
Par rapport la base associe au sol le tronc 1
donc la hanche 3 est incline dÕun angle ![]() (fig. 15)
tel que
(fig. 15)
tel que ![]() .
.
Q
10 : Comparer les rsultats trouvs la question Q 9 et les rsultats donns par une
simulation du robot. Pour cela
¤ identifier et conclure quant aux
coordonnes articulaires ;
¤ retrouver les coordonnes ![]() et
et ![]() donnes sur la fig. 15 ;
donnes sur la fig. 15 ;
¤ vrifier approximativement la position
du point ![]() sur le robot ;
sur le robot ;
¤ conclure propos valeurs simules, mesures et calcules.
![]()
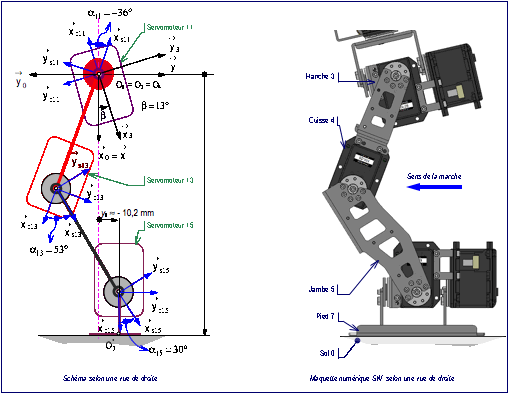
fig. 15 : Position de la jambe droite avant la marche (Ç Walkready È)
LÕexamen des donnes de lÕapplication
numrique de la question Q
9
et
des fig. 13 et fig. 15 permet de conclure que :
![]() et
et ![]()
mais que ![]() et
et ![]() , les signes opposs proviennent du choix du paramtrage (qui
pourrait tre modifi) et la diffrence de valeur, de lÕinclinaison du tronc de
+13¡ mais aussi que le pied doit rester en contact avec le sol. Tout cela est cohrent
dÕo
, les signes opposs proviennent du choix du paramtrage (qui
pourrait tre modifi) et la diffrence de valeur, de lÕinclinaison du tronc de
+13¡ mais aussi que le pied doit rester en contact avec le sol. Tout cela est cohrent
dÕo
![]()
Ces valeurs correspondent
approximativement celles donnes par la fig. 13.
Les coordonnes ![]() et
et ![]() donnes
dans le repre
donnes
dans le repre ![]() sur la fig. 15 diffrent des
valeurs de x et y exprimes dans le repre
sur la fig. 15 diffrent des
valeurs de x et y exprimes dans le repre ![]() car globalement le tronc est inclin de lÕangle
car globalement le tronc est inclin de lÕangle![]() .
.
Pour retrouver la position de ![]() on peut crire
on peut crire
avec ![]()
![]()
![]()
soit ![]()
comme ![]()
![]()
Alors avec les rsultats prcdents on
obtient
![]()
![]()
![]()
![]()
dÕo avec ![]()
alors ![]()
![]()
Comme ![]() et
et ![]()
en posant ![]()
alors ![]()
![]()
LÕorientation du pied 7 par rapport au
sol 0 est telle que
![]()
![]()
![]() le pied est en
contact avec le sol.
le pied est en
contact avec le sol.
DOSSIER
REPONSES (doc. Etudiant)
Postes 1 et 2
Rponse Q 4 :
Postes 3 et 4
Rponse Q 4 :
DOSSIER REPONSES (doc. Professeur)
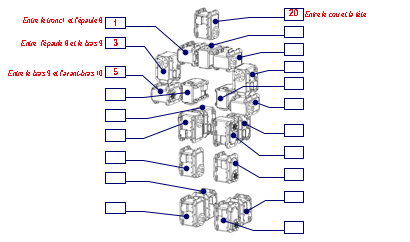
Postes 1 et 2
Rponse Q 4 :
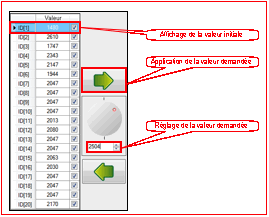
La valeur initiale donne pour le servomoteur 1 qui commande
lÕpaule 8 par rapport au tronc 1 est de 1480 points. Pour tourner de +90¡, il
faut ajouter 90/0,0879 points soit environ 1024 points. Il faut donc entrer la
valeur de 1480+1024 = 2504 points.
Postes 3 et 4
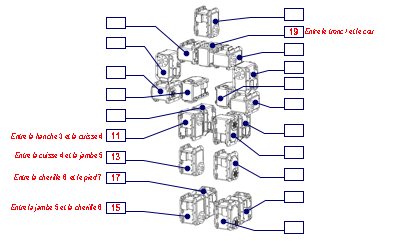
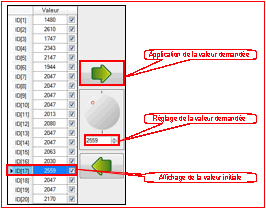
Rponse Q 4 :
La valeur initiale donne pour ce
servomoteur 17 qui commande le pied 7 par rapport la cheville 6 est de 2047 points.
Pour tourner de +45¡, il faut ajouter 45/0,0879 points soit environ 512 points.
Il faut donc entrer la valeur de 2047+512 = 2559 points.
REPONSE
TECHNIQUE (doc. Etudiant)
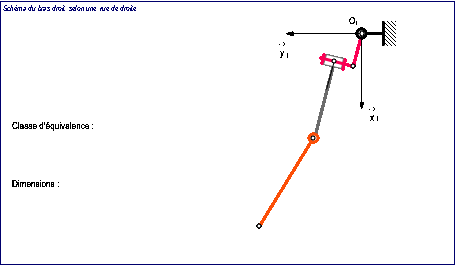
Postes 1 et 2
Postes 3 et 4
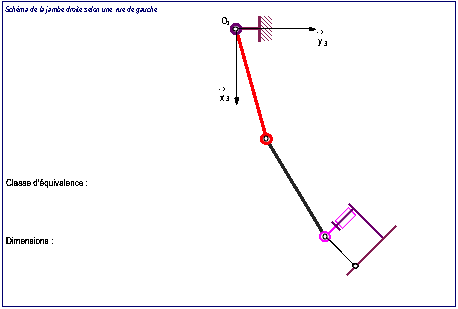
REPONSE
TECHNIQUE (doc. Professeur)
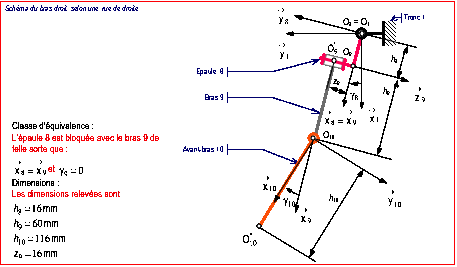
Postes 1 et 2
Les relations (1) et (2) fournissent les
coordonnes cartsiennes du point ![]() dans le repre
dans le repre ![]()
![]() (1)
(1)
![]() (2)
(2)
LÕavant-bras 10 par rapport au torse 1
est globalement orient par
![]()
Postes 3 et 4
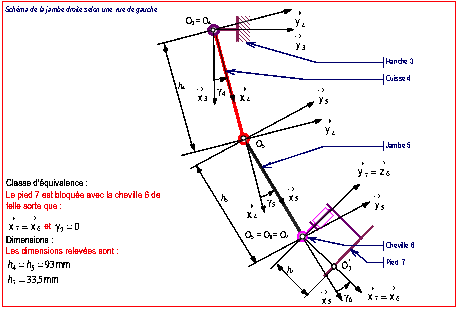
Les relations (1) et (2) fournissent les
coordonnes cartsiennes du point ![]() dans le repre
dans le repre ![]()
![]() (1)
(1)
![]() (2)
(2)
LÕorientation du pied 7 est fixe par
![]()
donc en appliquant la relation de Chasles
sur les angles
![]() (3)
(3)
FICHE
DE FORMALISATION (doc. Professeur)
1.La
premire tape de lÕtude gomtrique dÕun systme mcanique consiste dfinir
le schma cinmatique minimal.
2.La
deuxime tape sÕtablit partir du schma cinmatique, pour paramtrer :
¤
les solides
en associant un repre chaque solide Si et en dfinissant dans
chaque repre la position des centres de liaison par des paramtres
gomtriques constants ; un des vecteurs unitaires est associ lÕaxe de
la liaison et le centre du repre est plac sur cet axe ;
¤
les liaisons
en associant chacune dÕelle les paramtres gomtriques variables qui
correspondent aux degrs de libert (ou coordonnes articulaires).
3.La
troisime tape de lÕtude gomtrique dÕun systme mcanique constitu de solides en chane ouverte consiste
dfinir le modle gomtrique direct. Ce modle dcrit la position que
prend le segment terminal de la structure (effecteur) lorsque la valeur des
variables articulaires est connue, c'est--dire pour une configuration donne
de la structure. Ce modle est constitu de lÕexpression des coordonnes du
repre li au segment terminal dans le repre li au solide de rfrence,
exprim en fonction des coordonnes articulaires.
Dans
le plan pour exprimer le modle gomtrique direct on
applique la relation de Chasles aux positions et aux angles
AUTO-EVALUATION
DES SAVOIR-FAIRE
|
Savoir-faire
intermdiaire |
Acquis |
Je saurai refaire avec de l'aide |
Non acquis |
|
|
Paramtrage dans le plan |
Mettre en place les
origines des repres en privilgiant la gomtrie des liaisons |
|
|
|
|
Mettre en place les
repres associs aux solides en privilgiant la gomtrie des liaisons |
|
|
|
|
|
Placer les paramtres
constants lis aux solides |
|
|
|
|
|
Placer les coordonnes
articulaires associes aux liaisons |
|
|
|
|
|
Effectuer un changement
de base |
|
|
|
|
|
Ecrire le vecteur
position dÕun point |
|
|
|
|
|
Exprimer les coordonnes
cartsiennes dÕun point |
|
|
|
|
|
Utiliser la relation de
Chasles sur les positions |
|
|
|
|
|
Utiliser la relation de
Chasles sur les angles |
|
|
|
|
|
Savoir-faire du programme |
|
|
|
|
|
Associer un repre un solide |
|
|
|
|
|
Identifier les degrs de libert
dÕun solide en mouvement par rapport un repre |
|
|
|
|
|
Raliser le paramtrage dÕun
mcanisme simple |
|
|
|
|
|
Prendre en compte les
restrictions de mouvement pour simplifier les modles |
|
|
|
|
|
Ecrire le vecteur position dÕun
point dÕun solide, dans le systme de coordonnes cartsiennes |
|
|
|
|